




黎曼流形上的深度学习及其应用
黎曼流形上的深度学习及其应用





江南大学

北京理工大学

意大利特伦托大学、德国马普所

北京理工大学
随着人工智能的快速发展,深度学习已经在计算机视觉、模式识别等领域取得了革命性的进展。然而,传统的深度学习范式主要构建在欧氏空间,忽视了现实世界中大量数据所天然具备的非欧几里得结构。例如,用于信号数据表示分析的协方差矩阵、子空间矩阵、曲率空间、高斯分布等特征描述符,均呈现出非欧几何的特性。这种不匹配性使得基于欧氏空间的深度学习网络在数据的建模、表征以及分类的过程中将无法充分地解析和利用数据的结构信息,从而影响了模型的性能。
黎曼流形作为刻画非欧几何结构的核心数学工具,为深度学习提供了新的理论框架与算子体系。借助黎曼几何、度量空间、黎曼参数优化等理论,研究者将欧氏深度学习中的一些基本运算(卷积、残差、注意力、批次归一化等)推广至黎曼流形范畴,并逐步设计出一系列的“黎曼深度学习”(Riemannian Deep Learning, RieDL)模型和算法。例如:
如图1所示,在多个科学与工程领域,如骨架行为识别、生物电信号(EEG、ECG等)解码、图像集分类、节点分类、医学图像分割等,大量的实验证据表明RieDL在理论上较之欧氏模型具有更加有效的表征能力。
因此,本次讲习班以“黎曼流形上的深度学习及其应用”为主题,旨在系统性的介绍黎曼流形与深度学习的结合方法、典型模型及前沿应用,搭建起数学理论与人工智能方法论之间的桥梁。
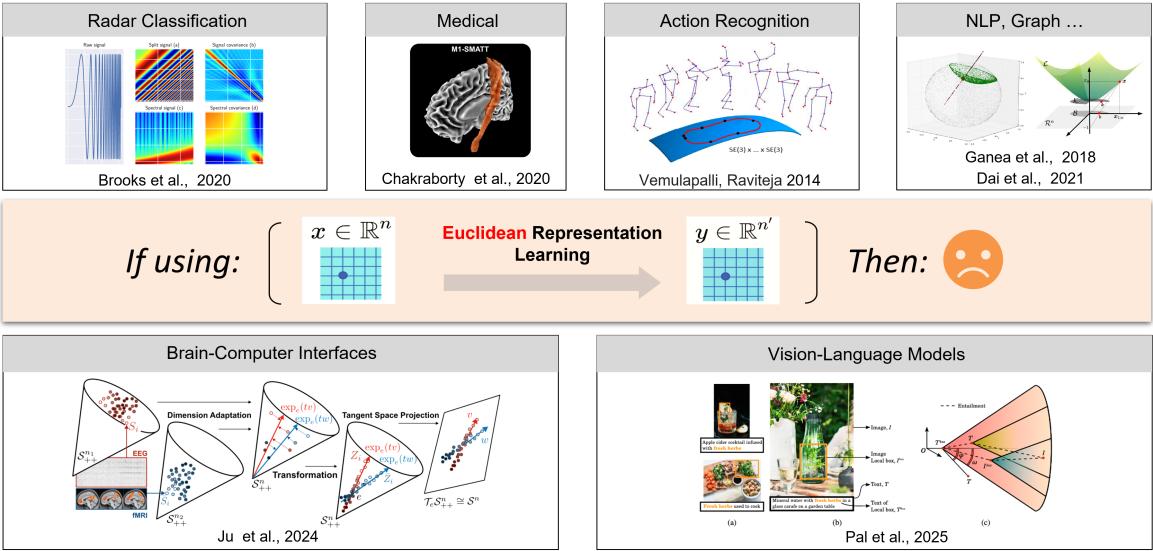
图1:在骨架行为识别、生物电信号(EEG、ECG等)解码、图像集分类、节点分类、医学图像分割等科学和工程领域,数据往往呈现出高维空间中所嵌入的低维流形结构。相较于传统的欧氏方法,黎曼深度学习能够在尊重数据内在几何结构的前提下,实现更为合理的建模、
表征与分类。
本次讲习班的主要目的可概括为以下三方面:
1. 系统性梳理黎曼深度学习的理论框架
在过去十年间,以黎曼流形为理论基础的几何深度学习方法得到了学术界的广泛关注,但该领域的知识体系较为零散,且仍处于发展初期。我们拟在本次讲习班中,以一种通识和直观的方式,从基础的黎曼几何概念出发,逐步展开:
通过这种讲解路径,帮助与会者建立从数学基础到深度模型的完整认知框架。
2. 搭建跨学科交流的平台
黎曼深度学习既需要数学理论的支撑,也需要对人工智能前沿问题的深入理解。通过此次讲习班,我们希望:
3. 展示应用前景与未来挑战
除理论介绍外,我们将结合大量前沿应用案例,展示黎曼深度学习在实际任务中的性能优势。同时,我们也将讨论其所面临的挑战,包括:
我们希望通过本次讲习班引导更多的科研工作者共同思考并探索下一代深度学习的可能路径。
1. 学术意义:迈向下一代深度学习新范式
当前深度学习已在多个应用领域趋于饱和,传统欧氏框架下的改进策略难以带来革命性突破。黎曼流形作为数学与人工智能交叉的重要桥梁,为深度学习注入了新的范式。
2. 应用意义:赋能关键科学与工程任务
黎曼深度学习的应用价值已经在多个领域初步显现:
这些应用的共同点是:数据通常具有高维、非线性、结构化特征,而黎曼流形恰是建模此类数据的天然舞台。
3. 社会意义:增强深度学习的可靠性与安全性
随着深度学习在医疗健康、自动驾驶、生物信息等关键领域的广泛应用,算法的可靠性与安全性已成为社会高度关注的焦点。黎曼深度学习通过利用和保持数据的本征非欧几何结构,能够显著提升模型的可信度:
因此,从社会角度看,黎曼深度学习不仅拓展了人工智能的理论边界,也为深度学习技术的安全落地提供了必要支撑。
综上所述,本次讲习班以“黎曼流形上的深度学习及其应用”为核心主题,目标是系统性梳理理论、搭建跨学科平台、展示前沿应用与挑战,其意义体现在探索学术前沿、赋能应用场景以及促进数学与AI的深度融合 。
我们相信,本讲习班的举办不仅能为与会者带来丰富的知识收获,也将为人工智能的下一代范式探索注入新的动力。黎曼深度学习有望成为未来人工智能发展的关键方向之一,而本次讲习班正是这一愿景的重要起点。
[1] Huang, Z., Van Gool, L.: A Riemannian Network for SPD Matrix Learning. In: AAAI. pp. 2036–2042 (2017).
[2] Huang, Z., Wu, J., Van Gool, L.: Building Deep Networks on Grassmann Manifolds. In: AAAI.
pp. 3279–3286 (2018).
[3] Zhang, T., Zheng, W., Cui, Z., Zong, Y., Li, C., Zhou, X., & Yang, J.: Deep Manifold-to-Manifold Transforming Network for Skeleton-Based Action Recognition. IEEE Trans. multimedia, 22(11), 2926-2937 (2020).
[4] Chakraborty, R., Bouza, J., Manton, J. H., Vemuri, B. C.: ManifoldNet: A Deep Neural Network for Manifold-Valued Data With Applications. IEEE Trans. Pattern Anal. Mach. Intell., 44(2), 799–810 (2022).
[5] Wang, R., Wu, X.J., Kittler, J.: SymNet: A Simple Symmetric Positive Definite Manifold Deep Learning Method for Image Set Classification. IEEE Trans. Neural Networks Learn. Syst, 33(5): 2208–2222 (2022).
[6] Chakraborty, R., Huang, A., Manton, J. H., Vemuri, B. C.: Riemannian Residual Networks. In: NeurIPS, 36, (2023).
[7] Wang, R., Wu, X.J., Chen, Z., Xu, T., Kittler, J.: DreamNet: A Deep Riemannian Manifold Network for SPD Matrix Learning. In: ACCV, pp. 3241–3257 (2022).
[8] Chami, I., Ying, Z., Ré, C., Leskovec, J.: Hyperbolic Graph Convolutional Neural Networks. In: NeurIPS, pp. 4869-4880 (2019).
[9] Zhao, W., Lopez, F., Riestenberg, J.M., Strube, M., Taha, D., Trettel, S. : Modeling Graphs Beyond Hyperbolic: Graph Neural Networks in Symmetric Positive Definite Matrices. In: ECML PKDD, pp.122–139 (2023).
[10] Pan, Y.T., Chou, J.L., Wei, C.S.: MAtt: A Manifold Attention Network for EEG Decoding. In: NeurIPS, pp. 31116–31129 (2022).
[11] Wang, R., Hu, C., Chen, Z., Wu, X.-J., Song, X.: A Grassmannian Manifold Self-Attention Network for Signal Classification. In: IJCAI, pp. 5099-5107 (2024).
[12] Hu, C., Wang, R., Song, X., Zhou, T., Wu, X.-J., Sebe, N., Chen, Z.: A Correlation Manifold Self-Attention Network for EEG Decoding. In: IJCAI (2025).
[13] Brooks, D., Schwander, O., Barbaresco, F., Schneider, J.Y., Cord, M.: Riemannian Batch Normalization for SPD Neural Networks. In: NeurIPS, pp. 15463–15474 (2019).
[14] Wang, R., Jin, S., Chen, Z., Luo, X., Wu, X.-J.: Learning to Normalize on the SPD Manifold under Bures-Wasserstein Geometry. In: CVPR, pp. 8289–8298 (2025).
[15] Chen, Z., Song, Y., Xu, T., Huang, Z., Wu, X.-J., Sebe, N.: Adaptive Log-Euclidean Metrics for SPD Matrix Learning. IEEE Trans. Image Process., 33(9), 5194–5205 (2024).
[16] Wang, R., Wu, X.-J., Chen, Z., Hu, C., Kittler, J.: SPD Manifold Deep Metric Learning for Image Set Classification. IEEE Trans. Neural Netw. Learn. Syst., 35(7), 8924–8938 (2024).
[17] Wang, R., Wu, X.-J., Xu, T., Hu, C., Kittler, J.: Deep Metric Learning on the SPD Manifold for Image Set Classification. IEEE Trans. Circuits Syst. Video Technol., 34(2), 663-680(2024).
[18] Dan, T., Huang, Z., Cai, H., Laurienti, P. J., & Wu, G.: Learning Brain Dynamics of Evolving Manifold Functional MRI Data Using Geometric-Attention Neural Network. IEEE Trans. Med.
Imaging, 41(10), 2752–2763 (2022).
[19] Attyé, A., Renard, F., Anglade, V., Krainik, A., Kahane, P., Mansencal, B., Coupé, P., Calamante, F., et al.: Data-driven normative values based on generative manifold learning for quantitative MRI. Scientific Reports, 14, 7563 (2024).
[20] Wang, R., Jin, J., Chen, Z., Wu, C., Wu, X.-J., Sebe, N.: Structural Topology Refinement Network for Skeleton-Based Action Recognition. IEEE Trans. Instrum. Meas., 74, 1–16 (2025)
[21] Sezer, E., Can, A.: Anomaly Detection in Crowded Scenes Using Log-Euclidean Covariance Matrix. In: VISIGRAPP, pp. 279–286 (2018).
[22] Fang, L., He, N., Li, S., Plaza, A.J., Plaza, J.: A New Spatial–Spectral Feature Extraction Method for Hyperspectral Images Using Local Covariance Matrix Representation. IEEE Trans. Geosci. Remote Sens, 56(6), 3534–3546 (2018).
[23] Khan, R.R., Chlenski, P., Pe’er, I.: Hyperbolic Genome Embeddings. In: ICLR (2025).
[24] Windels, S. F. L., Błażewicz, J., Stougie, L., Pržulj, N., van Leeuwen, E., Stoševski, M.: Graphlet-Based Hyperbolic Embeddings Capture Evolutionary Dynamics in Genetic Networks. Bioinformatics, 40(11), btae650 (2024).
[25] Hua, Y., Xu, T., Song, X., Feng, Z., Wang, R., Zhang, W., Wu, X.-J.: R-DTI: Drug Target Interaction Prediction Based on Second-Order Relevance Exploration. In: AAAI, pp. 17368-17376 (2025).
中国图象图形学学会 (CSIG)
中国人工智能学会 (CAAI)
中国计算机学会 (CCF)
中国自动化学会 (CAA)
上海交通大学 (SJTU)
上海飞腾文化传播有限公司
AutoDL
华东师范大学

